数据平滑与去噪是数据预处理中的重要技术，主要用于减少数据中的噪声，提取更具代表性的信息，提升模型的稳定性和准确性。 在日常开发过程中，数据平滑和去噪在信号处理、时间序列分析、图像处理等领域得到广泛的应用。
平滑方法常见的有移动平均法、指数平滑法、卷积平滑法。移动平均法：最常用的平滑方法之一，通过计算一个滑动窗口内数据的平均值来消除随机波动。窗口越大，平滑效果越明显。（比如，股票市场中，股票价格的日常波动包含许多噪声，通过移动平均法可以平滑价格曲线，帮助投资者看清股票的长期趋势）指数平滑法：赋予较新的数据更高的权重，从而更快地响应数据中的趋势。通过指数衰减的方式对历史数据加权，逐步减小过去数据的影响。（比如，销售预测中，近期的数据更能反映当前趋势，因此使用指数平滑可以更好地预测未来销量）卷积平滑法：卷积运算是一种通过滑动一个核函数（如高斯核）与信号进行点积来平滑数据的技术，它通常用于信号处理和数据去噪。（卷积平滑在数据处理中比移动平均更灵活且更强大，因为它允许使用不同的核函数来捕捉数据的特性）这里我获取的是茅台在2025年11月1日到12月31日的日线股价数据，作平滑处理，在此之前需要安装Python的一个第三方库tushare 是一个开源的免费获取A股的股票、期货、基金等金融市场数据：pip install tushare
import tushare as ts# https://tushare.pro/ 注册有tokents.set_token('这里填写你的token')pro = ts.pro_api()# 获取股票数据df = pro.daily(ts_code='600519.SH', start_date='20251101', end_date='20251231')csv_file = 'guizhou_maotai_daily_20251101_20251231.csv'df.to_csv(csv_file, index=False)print("数据已保存到csv文件中")
保存的数据是不复权的数据，比如这里我截图，并比照12月10日的数据，注意右边那里圈出来的地方是不复权。（复权的目的是为了消除股本变化对股价的影响，真实反映股价的走势。不复权保留了原始的缺口，可能更适合观察实际的交易价格变化，但技术分析时可能因为缺口而不准确）左边的数据分别表示：股票代码、交易日期、开盘价、最高价、最低价、收盘价、前一个交易日的收盘价、涨跌额、涨跌幅、成交量、成交额。在现实应用中，和微积分密切相关的操作方法是卷积平滑法。在实际操作的过程中，卷积平滑处理的核心思想源于积分运算，尤其是连续卷积的公式：其中函数f和g是信号或核函数，通过滑动并求积分来平滑信号。在离散信号（这里的股票价格）中，这个积分简化为对一组离散点的加权平均计算。关于微积分，这里重点推荐一本零基础学微积分的漫画书，是一本小学生都可以看懂的微积分漫画：from matplotlib import pyplot as pltimport pandas as pdimport numpy as npimport tushare as tsfrom scipy.ndimage import convolve1d# 设置中文字体与负号显示plt.rcParams['font.sans-serif'] = ['SimHei']plt.rcParams['axes.unicode_minus'] = Falsecsv_file = 'guizhou_maotai_daily_20251101_20251231.csv'df = pd.read_csv(csv_file)# 定义一个高斯核函数，用于平滑kernel = np.array([0.25, 0.5, 0.25])# 使用高斯核平滑数据df['Smoothed_Close'] = convolve1d(df['close'], kernel)print(df[['trade_date','close','Smoothed_Close']])
trade_date close Smoothed_Close0 20251231 1377.18 1380.31501 20251230 1389.72 1389.65502 20251229 1402.00 1401.96253 20251226 1414.13 1411.10754 20251225 1414.17 1410.84255 20251224 1400.90 1405.95756 20251223 1407.86 1406.22007 20251222 1408.26 1408.59508 20251219 1410.00 1414.81509 20251218 1431.00 1426.275010 20251217 1433.10 1429.800011 20251216 1422.00 1425.775012 20251215 1426.00 1423.662513 20251212 1420.65 1419.822514 20251211 1411.99 1411.857515 20251210 1402.80 1404.650016 20251209 1401.01 1405.760017 20251208 1418.22 1416.865018 20251205 1430.01 1425.555019 20251204 1423.98 1426.767520 20251203 1429.10 1429.552521 20251202 1436.03 1437.290022 20251201 1448.00 1445.632523 20251128 1450.50 1449.075024 20251127 1447.30 1448.562525 20251126 1449.15 1447.562526 20251125 1444.65 1447.612527 20251124 1452.00 1453.812528 20251121 1466.60 1463.077529 20251120 1467.11 1467.957530 20251119 1471.01 1471.282531 20251118 1476.00 1473.502532 20251117 1471.00 1468.650033 20251114 1456.60 1463.645034 20251113 1470.38 1465.627535 20251112 1465.15 1464.917536 20251111 1458.99 1461.357537 20251110 1462.30 1454.230038 20251107 1433.33 1441.022539 20251106 1435.13 1430.917540 20251105 1420.08 1426.072541 20251104 1429.00 1428.270042 20251103 1435.00 1433.5000
csv_file = 'guizhou_maotai_daily_20251101_20251231.csv'df = pd.read_csv(csv_file)# 定义一个高斯核函数，用于平滑kernel = np.array([0.25, 0.5, 0.25])# 使用高斯核平滑数据df['Smoothed_Close'] = convolve1d(df['close'], kernel)plt.figure(figsize=(10, 6))df['trade_date'] = pd.to_datetime(df['trade_date'],format='%Y%m%d')plt.plot(df['trade_date'], df['close'], label='原始收盘价',color='blue',marker='o', markersize=3)plt.plot(df['trade_date'], df['Smoothed_Close'], label='平滑收盘价',color='red',marker='x', markersize=3)plt.title('贵州茅台日线收盘价与卷积平滑处理')plt.xticks(rotation=45)plt.xlabel('交易日')plt.ylabel('收盘价')plt.legend()plt.show()
整个代码也是比较简单，首先使用Pandas的read_scv读取我们开始获取的股价数据文件csv，然后定义一个简单的高斯核函数用于平滑处理，该核函数通过赋予中心数据点更大的权重来实现平滑效果，对相邻数据点的权重影响相对较小。然后使用scipy.ndimage中的convolve1d函数对收盘价列进行卷积操作，平滑后的数据被存储在新列df['Smoothed_Close'] 中，卷积操作通过滑动核函数对相邻数据进行加权平均，减少了数据中的噪声或短期波动。最后就是用Matplotlib进行可视化，分别绘制原始收盘价和平滑处理后的收盘价，设置不同的颜色和标记点，清楚地展示了数据的对比效果。在去噪算法中，微积分通过计算信号的导数，可以识别出信号的变化趋势和异常波动，从而实现去噪目的。具体来说，微积分可以通过平滑或过滤信号来减少噪声的影响，以便真实信号更清晰地呈现。微积分不仅可以分析信号的变化，还能识别和处理噪声，在实际应用中，常用的去噪方法包括高斯滤波和中值滤波。其中：G(x,y)是高斯核，表示在点(x,y)处的高斯函数值。σ是标准差，控制着高斯函数的宽度和形状，对平滑程度有直接影响。高斯滤波：基于高斯函数的线性平滑方法，其基本思想是用高斯函数加权邻域像素得到新的像素值。高斯滤波在空间域和频域中均可以实现，通常用于减少图像或信号中的高频噪声。中值滤波：一种非线性去噪方法，它通过取邻域像素的中值来替代中心像素的值。这种方法对脉冲噪声（如盐和胡椒噪声）特别有效，因为中值滤波可以有效地去除极端值的影响。（过程：确定窗口大小，选定当前像素的邻域，对邻域内的像素值进行排序，找到中间值，将当前像素值替换为中值）from matplotlib import pyplot as pltimport pandas as pdimport numpy as npimport tushare as tsfrom scipy.ndimage import gaussian_filter,median_filter# 设置中文字体与负号显示plt.rcParams['font.sans-serif'] = ['SimHei']plt.rcParams['axes.unicode_minus'] = False# 数据集：生成一个一维信号并添加噪声np.random.seed(42) # 保证结果的可重复性x = np.linspace(0,20,100)original_signal = np.sin(x) # 原始信号noisy_signal = original_signal + np.random.normal(0,0.5,size=x.shape) # 添加噪声# 高斯滤波sigma = 1 # 高斯核的标准差，控制平滑程度gaussian_smoothed = gaussian_filter(noisy_signal,sigma) # 使用高斯滤波器平滑信号# 中值滤波window_size = 5 # 中值滤波器的窗口大小median_smoothed = median_filter(noisy_signal, size=window_size) # 使用中值滤波器平滑信号# 绘制原始信号、添加噪声后的信号、高斯滤波后的信号和中值滤波后的信号plt.figure(figsize=(10,6))plt.subplot(1,2,1)plt.plot(x,original_signal,label='原始信号',color='blue',linewidth=2)plt.plot(x,noisy_signal,label='添加噪声后的信号',color='red',linewidth=2)plt.legend()plt.subplot(1,2,2)plt.plot(x,noisy_signal,label='原始噪声信号',color='red',linewidth=2)plt.plot(x,gaussian_smoothed,label='高斯滤波后的信号',color='green',linewidth=2)plt.plot(x,median_smoothed,label='中值滤波后的信号',color='blue',linewidth=2)plt.legend()plt.tight_layout()plt.show()
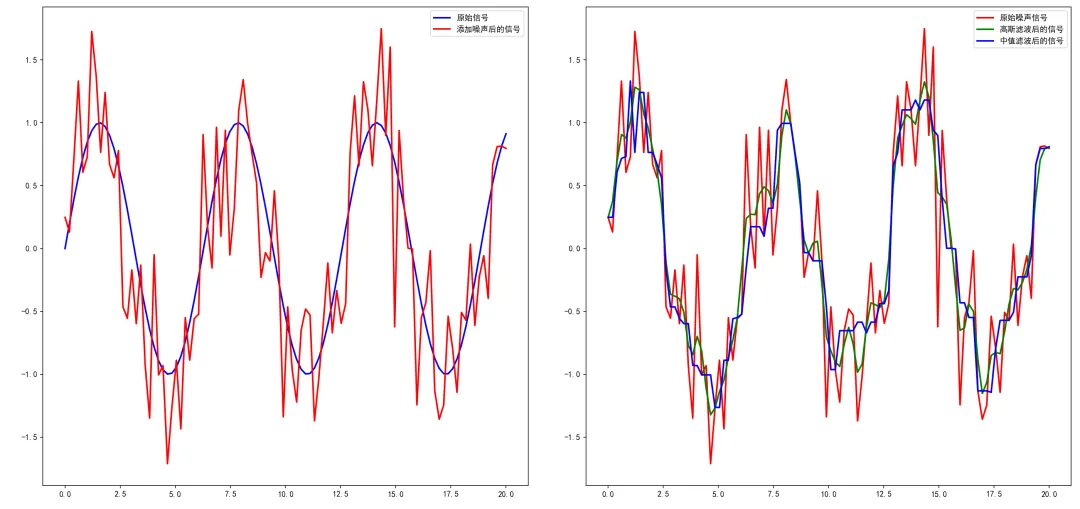这样就分别绘制出了带有2个子图的图片（plt.subplot(1,2,1)绘制1行2个的第一个图，plt.subplot(1,2,2)绘制1行2个的第二个图），左边的是原始信号和带噪声的信号，右边是经过高斯滤波和中值滤波平滑后的信号曲线。更多想要通过Python编程来理解微积分的朋友们，可以阅读《人工智能微积分基础》，这不是一本专门讲解微积分或者是编程的图书，而是将两者有机融合在一起，通过通俗易懂的解释以及自己编写代码的过程中，自然而然就掌握了微积分的应用和提高了编码能力。
