当前位置：首页>java>SQL编程大赛第5名周仟荣:用 PostgreSQL 位运算解决数独问题,碾压常规解法!

SQL编程大赛第5名周仟荣:用 PostgreSQL 位运算解决数独问题,碾压常规解法!

2026-01-23 05:54:41

数据库编程大赛：用一条 SQL 解数独问题

2025 NineData 第三届数据库编程大赛圆满举办！本次大赛由 NineData 和云数据库技术社区主办，并联合佰晟智算、达梦数据、 ITPUB、CSDN、IFclub、开源中国、DataFun、墨天轮等技术社区共同举办。本届大赛延续 "一条 SQL" 的核心挑战，设置题目为「用一条 SQL」解数独问题。查看赛题详情

以下是本次决赛第 5 名选手，周仟荣的参赛介绍：

第5名

周仟荣

参赛选手：周仟荣

选手简介：数据分析师，来自东风日产数据服务有限公司

参赛数据库：PostgreSQL

性能评测：1 万级数据代码性能评测 15.933 秒

综合得分：82.3

以下是周仟荣选手的代码说明思路简介：

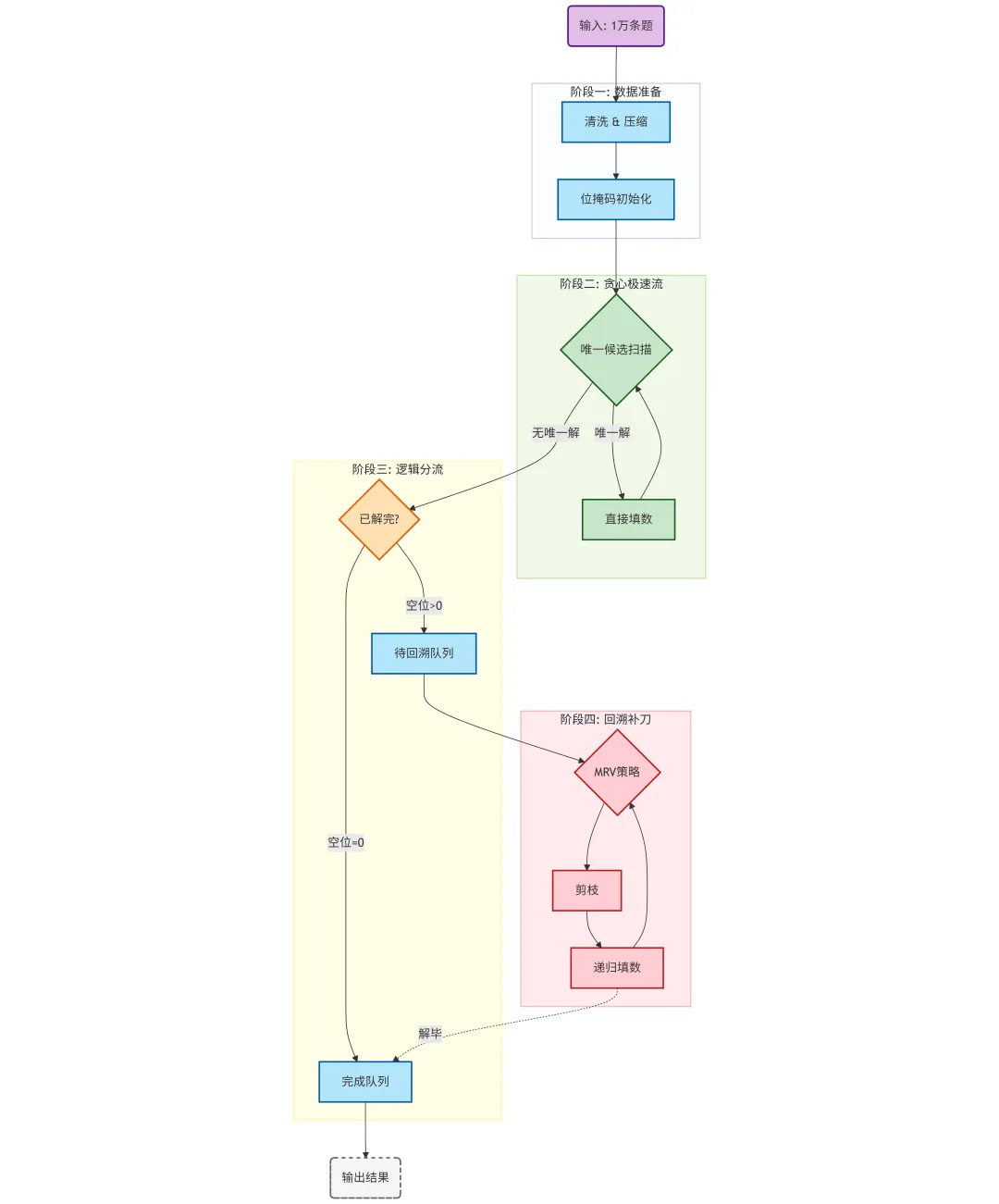
算法流程概览

数组高效构建棋盘
位掩码进行高效数据压缩和运算
分流策略：
1.简单题：具有唯一候选，快速扫描，不回溯
2.剩余难题：MRV策略进行剪枝
合并输出
FILTER、DISTINCT ON 等PostgreSQL特有语法的应用对性能有一定提升
延迟物化、内存压缩（Smallint）等优化对性能有提升

核心算法解析-位掩码

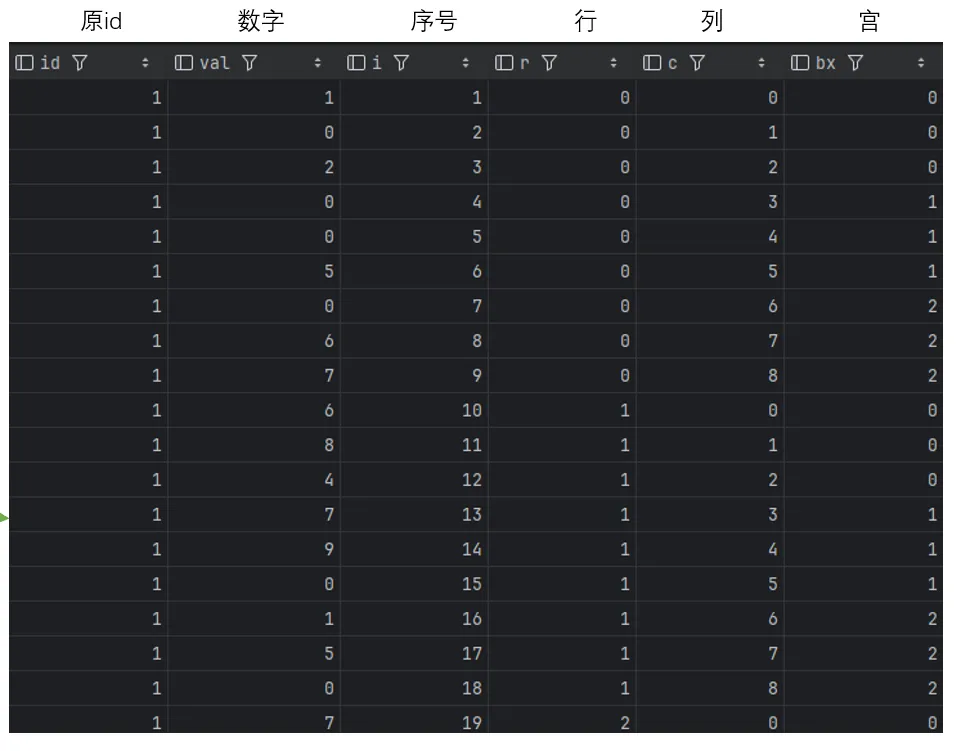
清洗、坐标构建

使用正则进行格式清洗，将待填空格替换为0

使用数组进行棋盘坐标构建

--示例生成中间表create  table dwd_sudoku_step1 asWITH RECURSIVE-- 1. 数据源 & 强壮解析 (Robust Parsing)src AS (    SELECT        id,        puzzle,        -- 【关键修复】：        -- 1. regexp_replace: 先暴力剔除所有非数字、非点、非问号的字符 (包括空格、换行、制表符等)        -- 2. translate: 再将 '.' 和 '?' 统一转为 '0'        -- 3. 结果: 得到纯净的 81 位数字字符串，绝对不会错位        string_to_array(            translate(                regexp_replace(puzzle, '[^0-9.?]', '', 'g'),                '.?', '00'            ),            NULL        )::smallint[] AS board    FROM sudoku9_9 --题面)-- 2. 棋盘单元格坐标构建    SELECT        id, val, i,   --id,原值,81位字符串序号        (i-1)/9 as r,   --行        (i-1)%9 as c,   --列        ((i-1)/27)*3 + ((i-1)%9)/3 as bx  --宫    FROM src, unnest(board) WITH ORDINALITY as t(val, i)  --数组展开为行;where id=1;

位图运算-1-二进制独热位掩码

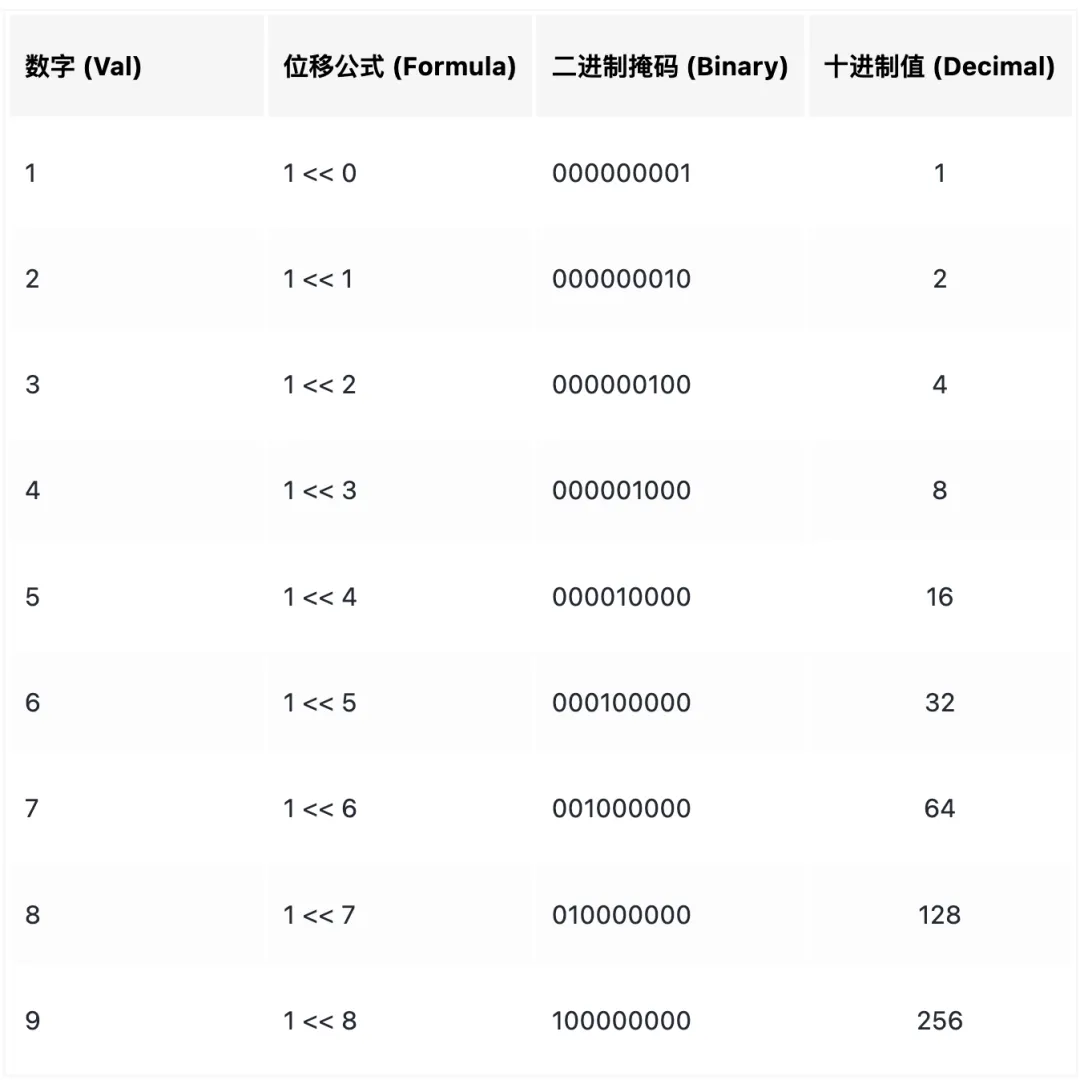
数字1~9位掩码:

利用 二进制独热位掩码 (Binary One-hot Bitmask) 技术，将棋盘 1-9 的十进制数值映射为特定的二进制位状态。

示例，第1行的已有数字 1、2、5、6、7 进行OR (|) 运算转为二进制掩码 001110011再转为10进制 115

--以第一行为例--棋盘数字转为二进制掩码SELECT    a.id           AS "ID",            --id    a.r + 1        AS "Row",          -- 行号    a.val         AS "Digit",         -- 数独数字    (1 << (a.val-1))          AS "Decimal", -- 十进制位状态    (1 << (a.val-1))::bit(9)  AS "Binary"   -- 二进制位状态FROM dwd_sudoku_step1 aWHERE a.id=1 AND a.val>0 AND a.r=0;--掩码 OR (|) 运算聚合SELECT    a.id           AS "ID",            --id    a.r + 1        AS "Row",          -- 行号    array_agg(a.val)        AS "Digit",         -- 数独数字    bit_or(1 << (a.val-1))          AS "Decimal", -- 十进制位状态    bit_or(1 << (a.val-1))::bit(9)  AS "Binary"   -- 二进制位状态FROM dwd_sudoku_step1 aWHERE a.id=1 AND a.val>0 AND a.r=0group by 1,2;

位图运算-2-行、列、宫已有数字掩码（黑名单）

以上示例拓展到行、列、宫，使用位掩码 bit_or (按位或) ,将每一行、列、宫中已有的数字记录在一个二进制数中,极大提升运算性能；

--Smallint更轻量计算速度更快

-- 3. 批量初始化掩码 (Filter 聚合)masks_calc AS (----使用“位掩码”技术。通过位运算（Bitwise OR）将每一行、列、宫中已有的数字记录在一个二进制数中    SELECT id, array_agg(COALESCE(m, 0)::smallint ORDER BY idx) as ms    FROM (        SELECT id, r+1 as idx, bit_or(1 << (val-1)) FILTER (WHERE val>0) as m FROM cells GROUP BY id, r        UNION ALL        SELECT id, c+10 as idx, bit_or(1 << (val-1)) FILTER (WHERE val>0) as m FROM cells GROUP BY id, c        UNION ALL        SELECT id, bx+19 as idx, bit_or(1 << (val-1)) FILTER (WHERE val>0) as m FROM cells GROUP BY id, bx    ) t    GROUP BY id),

结果为长度9*3=27的数组，分别表示行、列、宫各9组已有数字的掩码

位图运算-3-核心算法 — 位掩码与集合论 (Bitwise Set Theory)

Candidate=All(511)∩Not(Used)

即：

511& (Row∣Col∣Box)

1.聚合 (OR): 用 OR (|) 操作，把行、列、宫里用过的数字聚合，得到一个‘黑名单’。

2.取反 (NOT): 黑名单翻转为白名单，原来的黑名单变成了 0，而空闲的位置变成了 1。

但这里有个问题，计算机的整数是 32 位的，取反后高位全是 1（垃圾数据）。

3.过滤 (AND): 使用 511 (9个1) 筛除高位垃圾，锁定有效候选，只保留我们关心的 1-9 位。

4.以上只进行了3次计算即完成了一个格子的填充

以id=1为例，行、列、宫已有数字掩码聚合如下

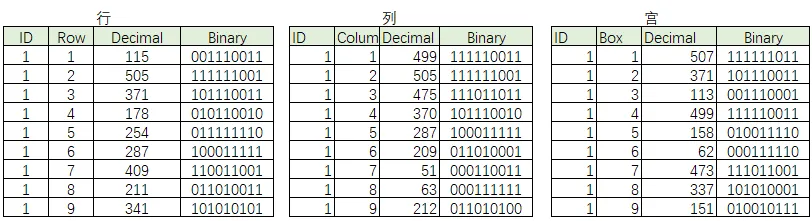
以取第1行第2列、第4列空格为例

已有数字掩码分别为 (115|505|507) 和 (115|370|371)，这两个空格可填数字计算如下

-- 遍历提取 (Iteration)-- 【核心特性】全量解析，结果完整-- 【适用场景】调试展示、回溯法分支生成 (需要所有可能性)WITH test_calc AS (    SELECT (511 & ~ (115|505|507)) as cand_m    union all    SELECT (511 & ~ (115|370|371)) as cand_m)SELECT    cand_m,    cand_m::bit(9) cand_m_bit,    (        SELECT string_agg(num::text, ',')        FROM generate_series(1, 9) num        WHERE (cand_m & (1 << (num - 1))) > 0 -- 挨个检查1-9是否在掩码里    ) as candidates_list,    bit_count(cand_m::bit(9)) bit_count   --掩码为1的数量FROM test_calc;

即快速求解出两个格子可填数字分别为3 和 3、4、8

注意：第一组仅有一个值，这是大部分简单题普遍情况，对于这种情况可以简化如下，只取首个值快速计算，避免消耗过多计算资源进行循环碰撞

-- 单值提取 (Bit Hack)，适用于只有唯一值时快速提取-- 【核心特性】极速计算，无循环-- 【适用场景】贪心阶段 (WHERE bit_count=1)，确保只有唯一解时使用WITH test_calc AS (    SELECT (511 & ~ (115|505|507)) as cand_m    union all    SELECT (511 & ~ (115|370|371)) as cand_m)select    a.cand_m,                          --十进制表达    a.cand_m::bit(9)  as cand_m_bit,   --二进制表达    -- 【关键逻辑】利用 x & -x 提取最低位的 1 (Lowbit)    -- 如果有多个候选数，这里会丢失高位数据，只返回最小的那个数字，需要限制仅存在唯一候选情况下使用，即掩码为1的数量=1    (bit_count(((a.cand_m & -a.cand_m) - 1)::bit(32)) + 1)::smallint candidates_list,  --可选数字    bit_count(cand_m::bit(9)) bit_countfrom test_calc a;

适用范围：仅存在唯一候选情况下使用，即掩码为1的数量=1

where bit_count(cand_m::bit(9))=1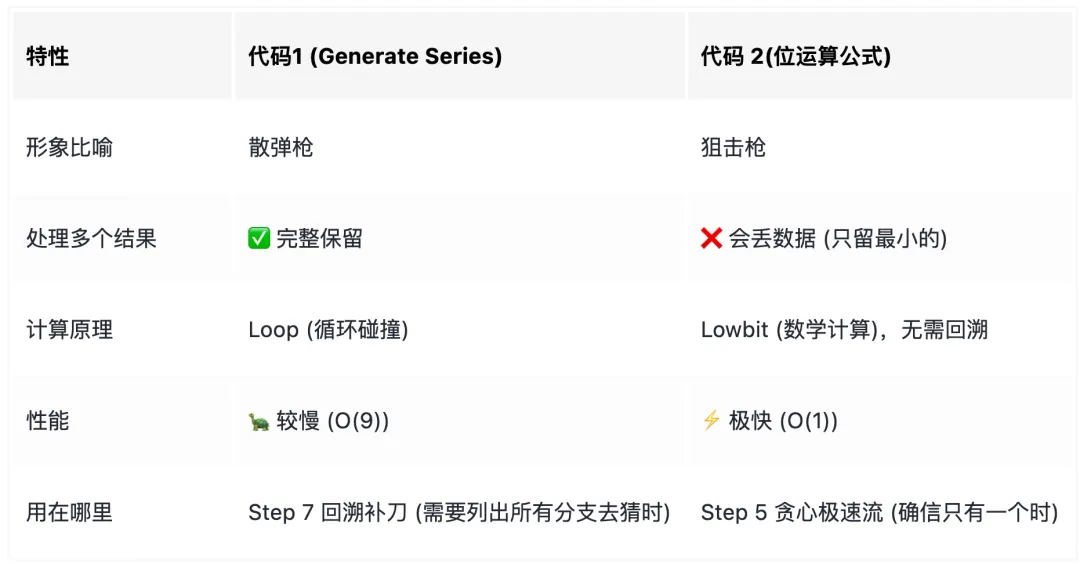

完整流程构建

待填格子位置索引

    ---待填格子位置索引：筛选出所有值为 0 的格子索引，打包为一个数组empty_calc AS (    SELECT id, array_agg(i::smallint ORDER BY i) as emp    FROM cells WHERE val = 0 GROUP BY id),

WHERE* val= 0:

•含义：这是过滤器。在数独逻辑中，0 代表空位（即原题中的 ? 或 .）。

•作用：只关心那些“需要填”的格子，忽略那些题目自带的已知数字（1-9）。

•i::smallint:

•含义：i 是格子在 81 个字符长字符串中的绝对位置（1-81）。

•作用：强制转换为 smallint（2字节整数）。内存优化的一部分，比默认的 int（4字节）省一半内存。

•ORDER BY i:

•含义：在打包数组时，按照位置先后排序。

•作用：保证任务列表的顺序是确定性的（从左上角到右下角）。这对于后续递归逻辑的稳定性非常重要。

•array_agg**(...) as emp**:

•含义：聚合函数。将多行数据“捏”成一行里的一个数组。

•结果：emp (Empty Cells) 字段。

递归前数据准备

-- 4. 组装初始状态--递归前数据准备prep AS (    SELECT        s.id, s.board,  --[零件1] 原始棋盘        -- [零件2] 约束掩码 (27个整数)        -- 这里包含了 9行+9列+9宫 的初始状态        COALESCE(m.ms, '{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}'::smallint[]) as ms,        -- [零件3] 待办空位数组 (递归的任务列表)        COALESCE(e.emp, '{}'::smallint[]) as emp    FROM src s     -- 将三个独立的数据流合并为一行    LEFT JOIN masks_calc m ON s.id = m.id    LEFT JOIN empty_calc e ON s.id = e.id),

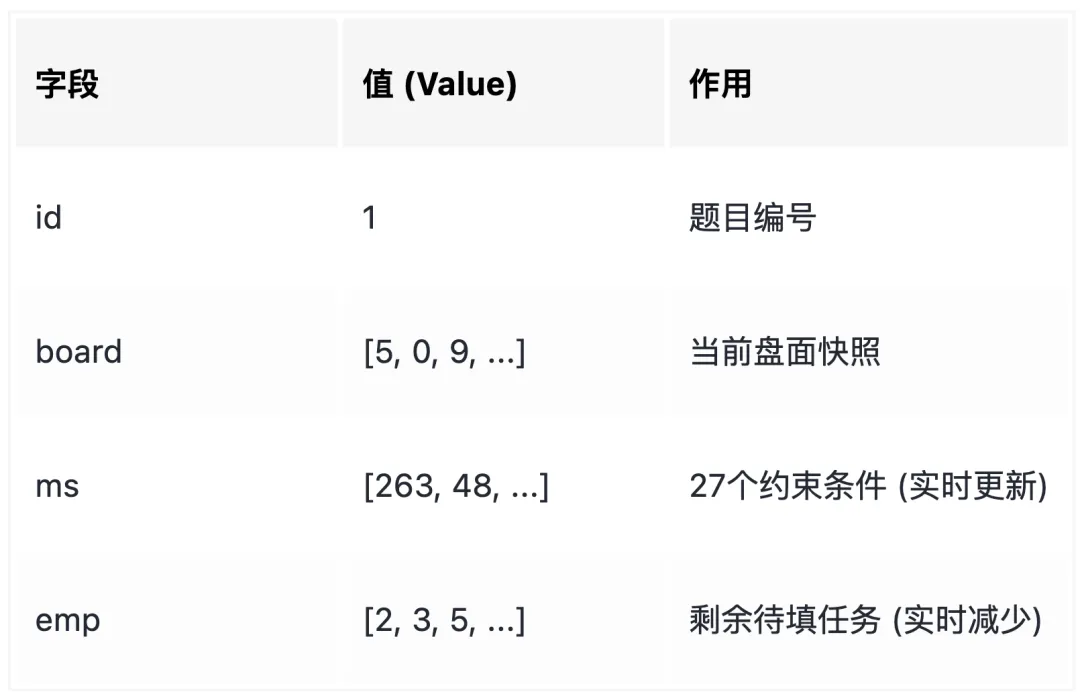
prep CTE 数据准备：

1.Board：当前的棋盘。

2.Masks：长度为27的位掩码数组，因为它一次性存储了 9****行+ 9****列+ 9****宫 的所有位掩码。

3.Emp：待填格子位置索引。

4.COALESCE 和 LEFT JOIN。为了代码的健壮性——即使输入的数独已经是满的（没有空位，empty_calc 为 NULL），代码也不会报错，而是生成一个空任务列表，直接流转到结束状态

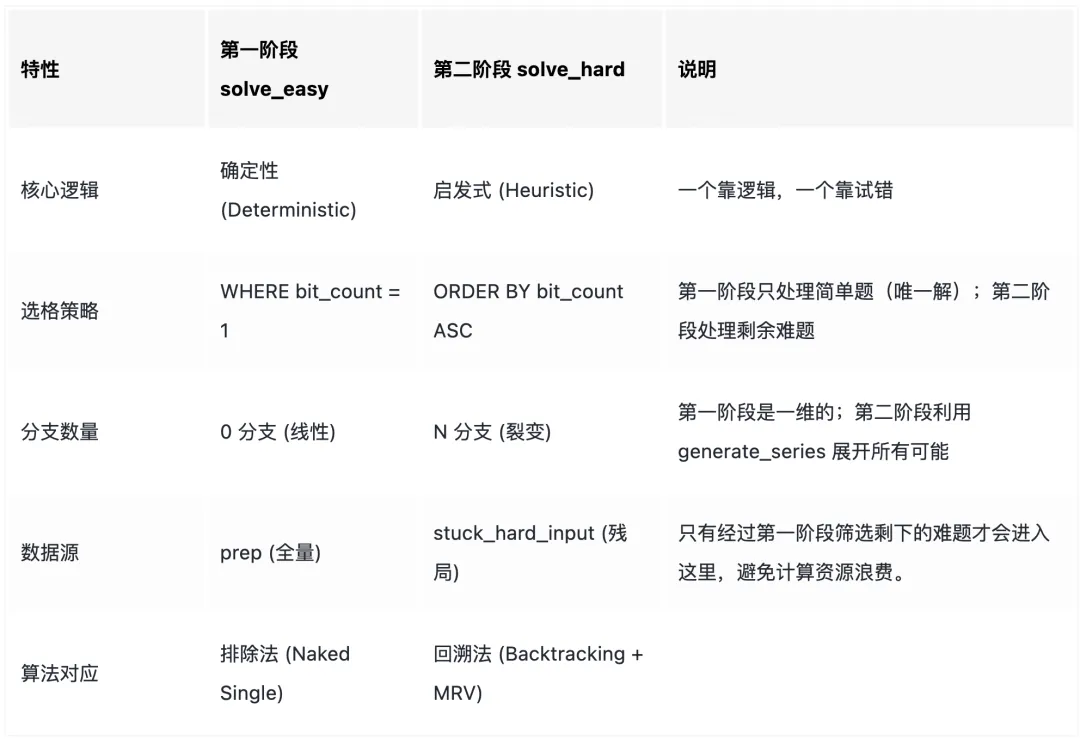
第一阶段简单题快速求解

-- 5. 第一阶段：贪心极速流 (确定性求解)solve_easy(id, board, ms, emp) AS (    SELECT id, board, ms, emp FROM prep    UNION ALL    SELECT        s.id,        -- 1. 更新棋盘：把原来的 0 替换成新的数字        s.board[:cell.p-1] || c.val::smallint || s.board[cell.p+1:],        -- 2. 更新掩码：把新数字加入到对应的行、列、宫的黑名单里        s.ms[:cell.r] || (s.ms[cell.r+1] | c.bit_m)::smallint || s.ms[cell.r+2:9+cell.c] || (s.ms[10+cell.c] | c.bit_m)::smallint || s.ms[11+cell.c:18+cell.bx] || (s.ms[19+cell.bx] | c.bit_m)::smallint || s.ms[19+cell.bx+1:27],        ---- 3.移除已处理空格：从空位列表里移除当前位置        array_remove(s.emp, cell.p)    FROM solve_easy s    INNER JOIN LATERAL (        SELECT p, (p-1)/9 as r, (p-1)%9 as c, (p-1)/27*3+(p-1)%9/3 as bx, cand_m        FROM unnest(s.emp) p   -- 展开所有空位(emp)        CROSS JOIN LATERAL (   -- 计算候选掩码：全集(511) 剔除(AND NOT) 行列宫已有的数字            SELECT 511 & ~(s.ms[(p-1)/9+1]::int | s.ms[(p-1)%9+10]::int | s.ms[(p-1)/27*3+(p-1)%9/3+19]::int) as cand_m        ) t        WHERE bit_count(cand_m::bit(9)) = 1     -- 【关键！】只要那些只有 1 个可能性的        LIMIT 1                                 -- 每次只抓一个，保持稳健    ) cell ON true    CROSS JOIN LATERAL (        -- 把二进制掩码转回 1-9 的十进制整数        SELECT (bit_count(((cell.cand_m & -cell.cand_m) - 1)::bit(32)) + 1)::smallint as val,               (cell.cand_m & -cell.cand_m)::int as bit_m    ) c),

A.扫描与计算(The Scanner)

•核心代码：511 & ~(Row | Col | Box)

•利用位运算瞬间计算补集。这相当于问数据库：在这个位置，除了行、列、宫里已有的数字，还剩下什么能填？

B.贪心判定(The Filter)

•代码：WHERE bit_count(...) = 1

•只有当某个格子在逻辑上只能填入一个数字时才行动。这保证了这一阶段的所有操作都是100% 正确的，不需要回溯。

C.状态更新(The Update)

•代码：s.ms[...] || ... (复杂的数组拼接)

•使用PostgreSQL 的数组切片操作，在填入数字时同时更新了行、列、宫的位掩码。这确保了下一次递归时，约束条件是最新的。

逻辑分流

-- 6. 逻辑分流finished_easy AS (    -- [快速通道] 只要任务清单空了，直接结算，释放内存    SELECT id, board FROM solve_easy WHERE cardinality(emp) = 0),stuck_hard_input AS (    -- [优胜劣汰] 筛选出卡住的难题    SELECT DISTINCT ON (id) id, board, ms, emp    FROM solve_easy    WHERE id NOT IN (SELECT id FROM finished_easy)    -- [关键策略] 如果有多个中间状态，取剩余空位最少的那一个继续算    ORDER BY id, cardinality(emp) ASC),

A.内存保护(Memory Safety)

•面对 1 万道题，如果让已完成的题目继续参与后续的递归连接，会造成巨大的内存浪费。通过 finished_easy 立刻卸载已完成的数据，相当于给系统做了‘内存减负’，防止大数据量下的磁盘溢出

B.优胜劣汰(Best-First Selection)

•在第一阶段，可能会产生同一题目的不同中间状态。利用 ORDER BY cardinality ASC，强行只保留完成度最高的那一个状态进入下一轮。这确保了后续的回溯搜索是从最佳起点开始的。

• PostgreSQL 特有的 DISTINCT ON 语法(比排序后limit 1高)

第二阶段-剩余难题处理--回溯补刀 (MRV 策略)

-- 7. 第二阶段：回溯补刀 (MRV 策略)solve_hard(id, board, ms, emp) AS (    SELECT id, board, ms, emp FROM stuck_hard_input  -- 接力棒：处理剩余的难题    UNION ALL    SELECT        s.id,        s.board[:cell.p-1] || v.val::smallint || s.board[cell.p+1:],        s.ms[:cell.r] || (s.ms[cell.r+1] | v.bit_m)::smallint || s.ms[cell.r+2:9+cell.c] || (s.ms[10+cell.c] | v.bit_m)::smallint || s.ms[11+cell.c:18+cell.bx] || (s.ms[19+cell.bx] | v.bit_m)::smallint || s.ms[19+cell.bx+1:27],        array_remove(s.emp, cell.p)    FROM solve_hard s    JOIN LATERAL (        SELECT p, (p-1)/9 as r, (p-1)%9 as c, (p-1)/27*3+(p-1)%9/3 as bx, cand_m        FROM unnest(s.emp) p        CROSS JOIN LATERAL (            SELECT 511 & ~(s.ms[(p-1)/9+1]::int | s.ms[(p-1)%9+10]::int | s.ms[(p-1)/27*3+(p-1)%9/3+19]::int) as cand_m        ) t        -- 【关键差异】不再寻找唯一解，而是寻找"可能性最少"的格子        ORDER BY bit_count(cand_m::bit(9)) ASC        LIMIT 1    ) cell ON true    JOIN LATERAL (        -- 【关键差异】展开所有可能的候选数        SELECT d+1 as val, 1<<d as bit_m        FROM generate_series(0,8) d WHERE (cell.cand_m & (1<<d)) <> 0    ) v ON true)

最终合并输出

-- 8. 最终合并输出SELECT    f.id,    s.puzzle,   -- [延迟物化] 此时才去读取原始题面字符串，而非在复杂递归中带着消耗资源    -- f.board,  --结果数组，方便验证数据，最终输出时注释掉    -- 格式化输出: 数组转字符串，每9位换行    trim(both E'\n' FROM regexp_replace(array_to_string(f.board, ''), '(.{9})', '\1' || E'\n', 'g')) as resultFROM (    SELECT id, board FROM finished_easy    UNION ALL    -- [去重] 再次确保每题只留一个解    SELECT DISTINCT ON (id) id, board FROM solve_hard WHERE cardinality(emp) = 0 ORDER BY id) fJOIN src s ON f.id = s.id;

A.延迟物化(Late Materialization)

在之前所有的递归计算中，没有携带 puzzle 这个原始字符串。因为字符串在内存中很占空间，且拷贝成本高。只传递了 ID 和轻量级的 smallint 数组。直到最后一步，才通过 JOIN 把它拿回来。这种延迟物化策略，可以节省一些内存提升性能。

B.结果整形(Result Formatting)

•利用了 PostgreSQL 强大的正则替换功能。 (.{9}) 匹配任意 9 个字符，\1\n 在其后插入换行符。这避免了写复杂的循环或应用层代码，直接在数据库层完成了数据的渲染

参赛完整SQL：

--用一条 SQL 解数独问题--数据库：PostgreSQL--提交人：周仟荣1WITH RECURSIVE-- 1. 数据源 & 强壮解析 (Robust Parsing)src AS (    SELECT        id,        puzzle,        -- 1. regexp_replace: 剔除所有非数字、非点、非问号的字符 (包括空格、换行、制表符等)        -- 2. translate: 再将 '.' 和 '?' 统一转为 '0'        -- 3. 结果: 得到纯净的 81 位数字字符串        string_to_array(            translate(                regexp_replace(puzzle, '[^0-9.?]', '', 'g'),                '.?', '00'            ),            NULL        )::smallint[] AS board    FROM sudoku9_9 -- 题面),-- 2. 拆解单元格坐标cells AS (    SELECT        id, val, i,   --id,原值,81位字符串序号        (i-1)/9 as r,   --行        (i-1)%9 as c,   --列        ((i-1)/27)*3 + ((i-1)%9)/3 as bx  --宫    FROM src, unnest(board) WITH ORDINALITY as t(val, i)   --数组展开为行),-- 3. 批量初始化掩码 (Filter 聚合)masks_calc AS (----使用“位掩码”技术。通过位运算（Bitwise OR）将每一行、列、宫中已有的数字记录在一个二进制数中    SELECT id, array_agg(COALESCE(m, 0)::smallint ORDER BY idx) as ms    FROM (        SELECT id, r+1 as idx, bit_or(1 << (val-1)) FILTER (WHERE val>0) as m FROM cells GROUP BY id, r        UNION ALL        SELECT id, c+10 as idx, bit_or(1 << (val-1)) FILTER (WHERE val>0) as m FROM cells GROUP BY id, c        UNION ALL        SELECT id, bx+19 as idx, bit_or(1 << (val-1)) FILTER (WHERE val>0) as m FROM cells GROUP BY id, bx    ) t    GROUP BY id),    ---待填格子位置索引：筛选出所有值为 0 的格子索引，打包为一个数组empty_calc AS (    SELECT id, array_agg(i::smallint ORDER BY i) as emp    FROM cells WHERE val = 0 GROUP BY id),-- 4. 组装初始状态--递归前数据准备prep AS (    SELECT        s.id, s.board,  --[零件1] 原始棋盘        -- [零件2] 约束掩码 (27个整数)        -- 这里包含了 9行+9列+9宫 的初始状态        COALESCE(m.ms, '{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}'::smallint[]) as ms,        -- [零件3] 待办空位数组 (递归的任务列表)        COALESCE(e.emp, '{}'::smallint[]) as emp    FROM src s     -- 将三个独立的数据流合并为一行    LEFT JOIN masks_calc m ON s.id = m.id    LEFT JOIN empty_calc e ON s.id = e.id),-- 5. 第一阶段：贪心极速流 (确定性求解)solve_easy(id, board, ms, emp) AS (    SELECT id, board, ms, emp FROM prep    UNION ALL    SELECT        s.id,        -- 1. 更新棋盘：把原来的 0 替换成新的数字        s.board[:cell.p-1] || c.val::smallint || s.board[cell.p+1:],        -- 2. 更新掩码：把新数字加入到对应的行、列、宫的黑名单里        s.ms[:cell.r] || (s.ms[cell.r+1] | c.bit_m)::smallint || s.ms[cell.r+2:9+cell.c] || (s.ms[10+cell.c] | c.bit_m)::smallint || s.ms[11+cell.c:18+cell.bx] || (s.ms[19+cell.bx] | c.bit_m)::smallint || s.ms[19+cell.bx+1:27],        ---- 3.移除已处理空格：从空位列表里移除当前位置        array_remove(s.emp, cell.p)    FROM solve_easy s    INNER JOIN LATERAL (        SELECT p, (p-1)/9 as r, (p-1)%9 as c, (p-1)/27*3+(p-1)%9/3 as bx, cand_m        FROM unnest(s.emp) p   -- 展开所有空位(emp)        CROSS JOIN LATERAL (   -- 计算候选掩码：全集(511) 剔除(AND NOT) 行列宫已有的数字            SELECT 511 & ~(s.ms[(p-1)/9+1]::int | s.ms[(p-1)%9+10]::int | s.ms[(p-1)/27*3+(p-1)%9/3+19]::int) as cand_m        ) t        WHERE bit_count(cand_m::bit(9)) = 1     -- 【关键！】只要那些只有 1 个可能性的        LIMIT 1                                 -- 每次只抓一个，保持稳健    ) cell ON true    CROSS JOIN LATERAL (        -- 把二进制掩码转回 1-9 的十进制整数        SELECT (bit_count(((cell.cand_m & -cell.cand_m) - 1)::bit(32)) + 1)::smallint as val,               (cell.cand_m & -cell.cand_m)::int as bit_m    ) c),-- 6. 逻辑分流finished_easy AS (    -- [快速通道] 只要任务清单空了，直接结算，释放内存    SELECT id, board FROM solve_easy WHERE cardinality(emp) = 0),stuck_hard_input AS (    -- [优胜劣汰] 筛选出卡住的难题    SELECT DISTINCT ON (id) id, board, ms, emp    FROM solve_easy    WHERE id NOT IN (SELECT id FROM finished_easy)    -- [关键策略] 如果有多个中间状态，取剩余空位最少的那一个继续算    ORDER BY id, cardinality(emp) ASC),-- 7. 第二阶段：回溯补刀 (MRV 策略)solve_hard(id, board, ms, emp) AS (    SELECT id, board, ms, emp FROM stuck_hard_input  -- 接力棒：处理剩余的难题    UNION ALL    SELECT        s.id,        s.board[:cell.p-1] || v.val::smallint || s.board[cell.p+1:],        s.ms[:cell.r] || (s.ms[cell.r+1] | v.bit_m)::smallint || s.ms[cell.r+2:9+cell.c] || (s.ms[10+cell.c] | v.bit_m)::smallint || s.ms[11+cell.c:18+cell.bx] || (s.ms[19+cell.bx] | v.bit_m)::smallint || s.ms[19+cell.bx+1:27],        array_remove(s.emp, cell.p)    FROM solve_hard s    JOIN LATERAL (        SELECT p, (p-1)/9 as r, (p-1)%9 as c, (p-1)/27*3+(p-1)%9/3 as bx, cand_m        FROM unnest(s.emp) p        CROSS JOIN LATERAL (            SELECT 511 & ~(s.ms[(p-1)/9+1]::int | s.ms[(p-1)%9+10]::int | s.ms[(p-1)/27*3+(p-1)%9/3+19]::int) as cand_m        ) t        -- 【关键差异】不再寻找唯一解，而是寻找"可能性最少"的格子        ORDER BY bit_count(cand_m::bit(9)) ASC        LIMIT 1    ) cell ON true    JOIN LATERAL (        -- 【关键差异】展开所有可能的候选数        SELECT d+1 as val, 1<<d as bit_m        FROM generate_series(0,8) d WHERE (cell.cand_m & (1<<d)) <> 0    ) v ON true)-- 8. 最终合并输出SELECT    f.id,    s.puzzle,   -- [延迟物化] 此时才去读取原始题面字符串，而非在复杂递归中带着消耗资源    -- f.board,  --结果数组，方便验证数据，最终输出时注释掉    -- 格式化输出: 数组转字符串，每9位换行    trim(both E'\n' FROM regexp_replace(array_to_string(f.board, ''), '(.{9})', '\1' || E'\n', 'g')) as resultFROM (    SELECT id, board FROM finished_easy    UNION ALL    -- [去重] 再次确保每题只留一个解    SELECT DISTINCT ON (id) id, board FROM solve_hard WHERE cardinality(emp) = 0 ORDER BY id) fJOIN src s ON f.id = s.id;

《数据库编程大赛》

下一次再聚！

感谢大家对本次《数据库编程大赛》的关注和支持，欢迎加入技术交流群，更多精彩活动不断，欢迎各路数据库爱好者来挑战！

本文来自网友投稿或网络内容，如有侵犯您的权益请联系我们删除，联系邮箱：wyl860211@qq.com 。

SQL编程大赛第5名周仟荣:用 PostgreSQL 位运算解决数独问题,碾压常规解法!

算法流程概览

核心算法解析-位掩码

清洗、坐标构建

位图运算-1-二进制独热位掩码

位图运算-2-行、列、宫已有数字掩码（黑名单）

位图运算-3-核心算法 — 位掩码与集合论 (Bitwise Set Theory)

完整流程构建

待填格子位置索引

递归前数据准备

第一阶段简单题快速求解

逻辑分流

第二阶段-剩余难题处理--回溯补刀 (MRV 策略)

最终合并输出

最新文章

热门文章

随机文章

SQL编程大赛第5名周仟荣:用 PostgreSQL 位运算解决数独问题,碾压常规解法!

算法流程概览

核心算法解析-位掩码

清洗、坐标构建

位图运算-1-二进制独热位掩码

位图运算-2-行、列、宫已有数字掩码（黑名单）

位图运算-3-核心算法 — 位掩码与集合论 (Bitwise Set Theory)

完整流程构建

待填格子位置索引

递归前数据准备

第一阶段简单题快速求解

逻辑分流

第二阶段-剩余难题处理--回溯补刀 (MRV 策略)

最终合并输出

Natrue│iVAC疫苗肿瘤内重编程癌细胞,癌症治疗的新技术

Python编程能力测评课 | 精准评估,科学规划,为孩子定制专属编程学习路径!

最新文章

热门文章

随机文章